수열과 집합의 합과 곱

데이터를 분석하기 위해서는 많은 숫자의 합이나 곱을 계산해야 한다.

따라서 숫자의 합과 곱을 나타내는 수학 기호에 익숙해지는 것은 데이터 분석의 첫걸음이다.

이 절에 나온 기호와 수식들은 앞으로 계속 반복하여 나오므로 반드시 외우고 손으로 여러 번 쓰기를 바란다.

 

수열과 집합의 합과 곱

 

수열                                                                                                              

수열(sequence)은 𝑁개 숫자 또는 변수가 순서대로 나열된 것이다. 다음은 수열의 예다.

 

 

 

문자에 붙은 아래 첨자는 순서를 나타내는 숫자로서 인덱스(index)라고 부른다.

수열이 아주 길거나 수열의 길이가 숫자가 아닌 문자인 경우에는 ……(dots) 기호를 사용하여 다음처럼 가운데 부분을 생략할 수 있다.

집합                                                                                                                                    

순서가 중요하지 않은 숫자들은 집합(set)으로 표시한다.

 

 

 

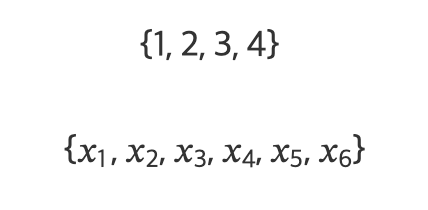
집합에서도 원소가 많으면 가운데를 생략할 수 있다.

 

데이터 분석에서는 1부터 𝑁까지의 수열 또는 집합이 자주 나오기 때문에 위에서 사용한 기호 대신

다음과 같이 더 간단한 기호를 쓰는 경우도 많다.

 

 

 

 

집합에 알파벳 대문자로 이름을 붙일 수도 있다.

데이터 분석에서 자주 나오는 집합 중의 하나는 1, -2, 3.14와 같은 실수(real number) 전체의 집합이다.

실수 집합은 𝐑이라는 이름을 가진다. 어떤 숫자 𝑥가 실수이면 집합 𝐑에 포함되므로 다음과 같은 기호로 나타낸다.

 

 

만약 두 개의 숫자로 이루어진 숫자 쌍 (𝑥1, 𝑥2)가 있고 각각의 숫자 𝑥1, 𝑥2가 모두 실수라면 다음처럼 표시한다.

 

 

---

수열의 합과 곱                                                                                                            

다음 기호는 수열을 더하거나 곱하는 연산을 짧게 줄여 쓴 것이다. 그리스 문자의 시그마(Σ)와 파이(Π)를 본따서 만든 기호지만 시그마와 파이로 읽지 않고 영어로 썸(sum), 프로덕트(product)라고 읽는다. 합과 곱 기호 아래에는 인덱스의 시작값, 위에는 인덱스의 끝값을 표시한다. 곱셈은 알파벳 x와 혼동될 수 있기 때문에 𝑎×𝑏가 아니라 𝑎⋅𝑏와 같이 점(dot)으로 표시하거나 아예 생략한다.

 

 

 

 

 

 

더하기나 곱하기를 반복해서 써야할 때는 합과 곱 기호를 사용하면 수식이 간결하고 명확해진다.
예를 들어 1부터 4까지 더해야 하는 경우에는 다음처럼 쓴다.

 

 

만약 10부터 90까지 10씩 증가하는 수열을 모두 더해야 한다면 다음처럼 쓴다.

 

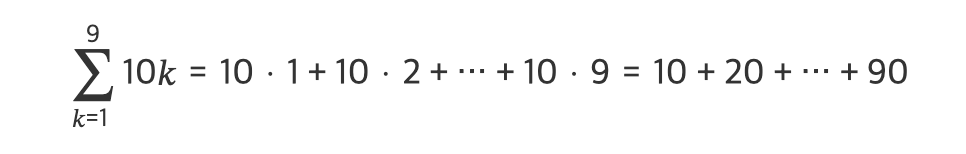
곱셈도 마찬가지이다. 다음은 10부터 20까지의 수를 모두 곱하는 식이다.

 

 

 

합이나 곱을 중첩하여 여러 번 쓰는 경우도 있다. 합과 곱을 중첩하여 쓸 때는 다음처럼 괄호를 생략할 수 있다.

합이나 곱이 중첩된 경우에는 인덱스가 여러 개가 된다.

 

 

 

다음은 합과 곱을 중첩한 수식의 예이다.

 

---

연습 문제 1.2.1

다음 수식을 풀어 써라. 이 수식들은 이후에 머신러닝 모형에 등장할 수식이다.

(1) 이 식은 분류 모형 중의 하나인 서포트 벡터 머신(support vector machine) 모형에 나온다.

 

 

(2) 이 식은 특잇값 분해(singular value decomposition)에 나온다.

 

(3) 이 식은 카테고리 분포(categorical distribution)의 추정에 사용된다.

 

 

(4) 가우시안 혼합 모형(Gaussian mixture model)에 다음과 비슷한 수식이 나온다.

 

 

연습 문제 1.2.2

수열의 곱은 여러개의 값 중 하나를 선택하는 경우에도 쓰일 수 있다. 수열 𝑥𝑖가 다음과 같다고 하자.

 

이 값 중 하나만 선택하고 싶다면 다음처럼 모두 0이고 하나만 1인 수열 𝑦𝑖를 사용하면 된다.

 

(1) 𝑥𝑖와 𝑦𝑖가 위와 같을 때 다음 값을 계산하라.

 

 

 

(2) 만약 수열 𝑦𝑖에서 𝑦3=1이고 나머지값이 0이라면 답이 어떻게 달라지는가? 

- 동일한 로직을 거쳐 X3만 남음.

 

수열의 합과 곱 연산은 다음과 같은 성질을 가지고 있다.

 

(1) 인덱스 문자가 바뀌어도 실제 수식은 달라지지 않는다.

 

 

 

(2) 상수 𝑐를 곱한 후에 합을 한 결과는 먼저 합을 구하고 상수를 곱한 것과 같다.

 

 

 

 

(3) 더해야 하는 값들이 여러 항의 합으로 되어 있으면 각각의 합을 먼저 구한 후에 더해도 된다.

 

 

 

(4) 합이나 곱을 중첩하는 경우에는 중첩의 순서를 바꾸어도 결과가 같다.

 

 

 

예를 들어 다음 두 식은 항들의 순서만 바뀌었고 그 합은 같다는 것을 알 수 있다.

 

 

  

연습 문제 1.2.3

 

다음 두 식의 좌변과 우변이 같음을 증명하라. (힌트: 등호의 왼쪽과 오른쪽 각각의 식을 풀어서 같아짐을 보인다.)

이 수식들은 선형대수에서 벡터 및 행렬의 곱에 유용하게 사용된다.

 

(1)

 

(2)

 

집합의 합과 곱                                                                                                                                                             

수열이 아니라 집합의 원소들의 합과 곱을 구할 때는 인덱스 대신 집합 기호를 사용한다.

만약 집합 𝑋의 원소가 다음과 같다면,

 

이 집합의 원소의 합과 곱은 다음처럼 표시한다. 이 때는 합과 곱 기호 안에 인덱스가 없다.

 

 

 

 

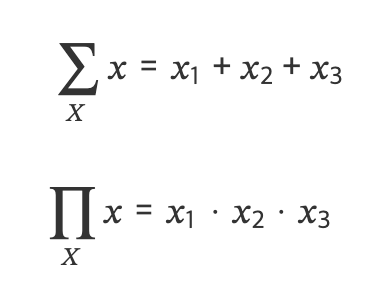
원소 중에서 특정한 조건을 가진 원소만 포함시키거나 제외하여 합과 곱을 구하는 경우도 있다.

이 때는 인덱스 위치에 조건을 표시한다. 예를 들어 다음 식은 집합 𝑋의 원소 중 0이 아닌 것만 곱한 값을 뜻한다.

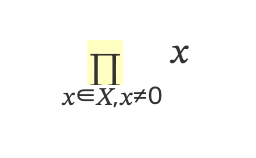
연습 문제 1.2.4

두 집합 𝑋1,𝑋2가 있고 𝑥1은 𝑋1의 원소들, 𝑥2은 𝑋2의 원소들을 가리킬 때 다음 두 식의 좌변과 우변이 같음을 증명하라.

문제를 간단하게 하기 위해 여기에서는 각각의 집합이 3개의 원소만 가지고 있다고 가정하자.

이 식의 확장된 버전은 추후 베이지안 네트워크의 합-곱(sum-product) 알고리즘에 사용된다.