내적(dot product)

내적(dot product)은 두 벡터 간의 연산으로, 두 벡터의 방향성과 크기를 기반으로 특정 값을 계산하는 방법입니다. 수학적으로, 내적은 두 벡터가 얼마나 비슷한 방향을 가지고 있는지와 관련이 있으며, 주로 벡터의 유사성을 측정할 때 사용됩니다.
1. 내적의 정의

즉, 각 성분을 곱한 값을 모두 더한 결과가 두 벡터의 내적입니다.
2. 기하학적 의미
내적은 두 벡터가 이루는 각도와 관련이 있습니다. 내적은 다음과 같은 식으로도 표현할 수 있습니다:
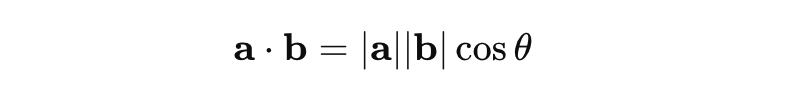
여기서:

따라서:

3. 내적의 특징
- 크기: 내적값이 클수록 두 벡터가 비슷한 방향을 가지고 있음을 의미합니다.
- 0: 내적값이 0이면 두 벡터가 수직임을 의미합니다.
- 유사성 측정: 내적은 특히 벡터의 유사성을 측정할 때 유용합니다. 이미지나 문서에서 벡터 표현을 통해 유사도를 측정할 수 있습니다.
예시

이 내적값 11은 두 벡터의 방향성과 크기 차이에 따른 유사성을 나타냅니다.
가중합(weighted sum)
내적은 *가중합(weighted sum)을 계산할 때도 매우 유용하게 사용됩니다. 가중합은 어떤 값들에 각각의 가중치를 곱한 후, 이들을 합산하는 것을 의미합니다. 내적 연산은 가중합을 구하는 과정과 동일한 방식으로 작동하기 때문에, 가중합 계산에 자주 사용됩니다.
가중합의 정의
가중합은 주어진 값들이 각각의 가중치를 가지며, 그 가중치에 따라 값들의 중요도가 달라질 때 사용됩니다.
예를 들어,

이 값들의 가중합은 다음과 같이 계산됩니다:
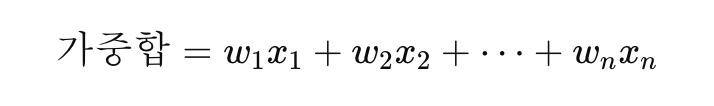
즉, 각 값에 해당하는 가중치를 곱하고, 그 결과들을 모두 더한 것입니다.
내적을 통한 가중합 계산
위의 가중합을 내적을 사용하여 계산할 수 있습니다. 벡터 𝑤와 𝑥의 내적을 구하면, 가중합을 구하는 것과 동일한 결과를 얻습니다.

따라서, 벡터 𝑤와 𝑥의 내적은 𝑥의 각 항목에 𝑤의 가중치를 곱한 값들의 합인 가중합을 계산하는 데 유용하게 사용됩니다.
예시
예를 들어, 학생의 시험 점수와 각 시험의 중요도가 주어졌을 때, 이를 가중합으로 계산해 종합 점수를 구할 수 있습니다.

이때 가중합을 계산하면:

따라서, 종합 점수는 86.5점이 됩니다. 이처럼 내적 연산은 가중치를 적용하여 합산하는 작업에서 매우 편리하게 사용됩니다.
요약
- 가중합: 각 값에 가중치를 곱한 후 합산한 것.
- 내적을 통한 가중합 계산: 두 벡터의 내적을 계산하여, 한 벡터의 값에 다른 벡터의 가중치를 적용한 합을 쉽게 구할 수 있습니다.
from sklearn.datasets import load_digits
import matplotlib.gridspec as gridspec
digits = load_digits()
d1 = digits.images[0]
d2 = digits.images[10]
d3 = digits.images[1]
d4 = digits.images[11]
v1 = d1.reshape(64, 1)
v2 = d2.reshape(64, 1)
v3 = d3.reshape(64, 1)
v4 = d4.reshape(64, 1)
plt.figure(figsize=(9, 9))
gs = gridspec.GridSpec(1, 8, height_ratios=[1],
width_ratios=[9, 1, 9, 1, 9, 1, 9, 1])
for i in range(4):
plt.subplot(gs[2 * i])
plt.imshow(eval("d" + str(i + 1)), aspect=1,
interpolation='nearest', cmap=plt.cm.bone_r)
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.title("image {}".format(i + 1))
plt.subplot(gs[2 * i + 1])
plt.imshow(eval("v" + str(i + 1)), aspect=0.25,
interpolation='nearest', cmap=plt.cm.bone_r)
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.title("vector {}".format(i + 1))
plt.tight_layout()
plt.show()
코드 설명 :
이 코드는 "0" 이미지와 "1" 이미지 간의 유사성을 내적(dot product)으로 비교하는 내용입니다.
내적값이 높을수록 두 벡터(이미지)가 서로 유사하고, 내적값이 낮을수록 두 벡터가 서로 다르다는 의미를 갖습니다.
코드를 살펴보면, load_digits() 함수로 숫자 이미지 데이터를 불러오고, 그 중 몇 가지 이미지를 선택하여 벡터로 변환했습니다. "0" 이미지와 "1" 이미지를 각각 두 개씩 선택하여 v1, v2 (0 이미지), v3, v4 (1 이미지)로 변환합니다. 각 이미지의 행렬 형태와 벡터 형태를 나란히 보여주기 위해 matplotlib의 GridSpec으로 시각화한 것입니다.
내적 값에 대한 설명
- 같은 숫자 이미지 간 내적값:
- (v1.T @ v2)[0][0]와 (v3.T @ v4)[0][0]는 "0" 이미지끼리와 "1" 이미지끼리의 내적입니다.
- 같은 숫자(0 또는 1) 이미지끼리 내적값이 높은 이유는 두 이미지가 매우 유사한 특징을 공유하기 때문입니다. 즉, "0" 이미지끼리, "1" 이미지끼리의 픽셀 값이 유사하여 내적값이 상대적으로 큽니다.
- 다른 숫자 이미지 간 내적값:
- (v1.T @ v3)[0][0], (v1.T @ v4)[0][0], (v2.T @ v3)[0][0], (v2.T @ v4)[0][0]는 "0" 이미지와 "1" 이미지 간의 내적입니다.
- "0"과 "1" 이미지는 형태가 다르기 때문에 픽셀 값도 다릅니다. 이러한 차이로 인해 서로 다른 숫자 이미지 간 내적값이 상대적으로 작게 나타납니다.
요약
- 같은 숫자끼리의 이미지 ("0"과 "0", "1"과 "1")의 내적값이 크고, 서로 다른 숫자끼리의 이미지 ("0"과 "1")의 내적값이 작은 이유는 픽셀 값의 유사성 때문입니다.
- 이처럼 같은 숫자는 비슷한 픽셀 패턴을 가지기 때문에 내적값이 높고, 다른 숫자는 패턴이 달라 내적값이 낮게 나옵니다.
이러한 내적 계산은 이미지의 유사성을 평가할 때 유용하며, 유사도가 높은 경우 내적값이 높게 나타나므로 해당 벡터들이 서로 유사한 특징을 많이 가지고 있다고 해석할 수 있습니다.
연습 문제 2.2.3
다음 코드를 실행하면 MNIST 숫자 이미지 전체 데이터를 모두 벡터로 변환하여 하나의 넘파이 행렬 X를 만든다. 이 행렬을 이용하여 다음 문제를 풀어라.

(1) 내적을 이용하여 첫 번째 이미지와 10번째 이미지의 유사도를 구하라.

(2) 내적을 이용하여 모든 이미지의 조합에 대해 유사도를 구하라. 어떻게 구현하는 것이 효율적일까? (힌트 : 이 문제는 뒤에서 배울 행렬과 행렬의 곱셈을 이용한다.)
[다시 업뎃]
'데싸를 위한 수학' 카테고리의 다른 글
| 내적과 외적의 차이 (1) | 2024.11.05 |
|---|---|
| 선형회귀 모형 (0) | 2024.11.05 |
| 넘파이(NumPy)로 공부하는 선형대수 (1) 데이터와 행렬 (6) | 2024.10.29 |
| 수열과 집합의 합과 곱 (2) | 2024.10.28 |
| 그리스 문자 - 수학의 변수 표기와 읽기 (4) | 2024.10.28 |



